Инструкция

Пусть тело брошено под углом α к горизонту с начальной скоростью v0. Начальные координаты тела пусть будут нулевыми: x(0)=0, y(0)=0. В проекциях на координатные оси начальная скорость разложится по двум составляющим: v0(x) и v0(y). То же самое скорости вообще. По оси Ox скорость условно считается постоянной, по оси Oy меняется под воздействием . Ускорение свободного падения g можно принять примерно за 10м/с².

Угол α, под которым брошено тело, задан не случайно. Через него можно расписать начальную скорость в координатных осях. Так, v0(x)=v0·cos(α), v0(y)=v0·sin(α). Теперь можно получить функцию координатных составляющих скорости: v(x)=const=v0(x)=v0·cos(α), v(y)=v0(y)-g·t=v0·sin(α)-g·t.

Координаты тела x и y зависят от времени t. Таким образом, можно составить два уравнения зависимости: x=x0+v0(x)·t+a(x)·t²/2, y=y0+v0(y)·t+a(y)·t²/2. Поскольку по x0=0, a(x)=0, то x=v0(x)·t=v0·cos(α)·t. Также известно, что y0=0, a(y)=-g (знак « » появляется оттого, что направление ускорения свободного падения g и положительное направление оси Oy противоположны). Поэтому y=v0·sin(α)·t-g·t²/2.

Время полета можно выразить из формулы скорости, зная, что в максимальной точке тело на мгновение останавливается (v=0), а длительности «подъема» и «спуска» равны. Итак, при подстановке v(y)=0 в уравнение v(y)=v0·sin(α)-g·t получается: 0=v0·sin(α)-g·t(p), где t(p) – пиковое время, «t вершинное». Отсюда t(p)=v0·sin(α)/g. Общее время полета тогда выразится как t=2·v0·sin(α)/g.

Ту же формулу можно получить и другим способом, математическим, из уравнения для координаты y=v0·sin(α)·t-g·t²/2. Это уравнение можно переписать в немного измененном виде: y=-g/2·t²+v0·sin(α)·t. Видно, что это квадратичная зависимость, где y – функция, t – аргумент. Вершиной параболы, описывающей траекторию, является точка t(p)=[-v0·sin(α)]/[-2g/2]. Минусы и двойки сокращаются, поэтому t(p)=v0·sin(α)/g. Если обозначить максимальную высоту за H и вспомнить, что пиковая точка является вершиной параболы, по которой движется тело, то H=y(t(p))=v0²sin²(α)/2g. То есть, чтобы получить высоту, надо «t вершинное» подставить в уравнение для координаты y.

Итак, время полета записывается как t=2·v0·sin(α)/g. Чтобы его изменить, надо соответственно менять начальную скорость и угол наклона. Чем больше скорость – тем дольше летит тело. С углом несколько сложнее, ведь время зависит не от самого угла, а от его синуса. Максимально возможное значение синуса – единица – достигается при угле наклона в 90°. Это означает, что дольше всего тело летит тогда, когда его бросают вертикально вверх.

Дальность полета является конечной координатой x. Если подставить найденное уже время полета в уравнение x=v0·cos(α)·t, то легко найти, что L=2v0²sin(α)cos(α)/g. Здесь можно применить тригонометрическую формулу двойного угла 2sin(α)cos(α)=sin(2α), тогда L=v0²sin(2α)/g. Синус двух альфа равен единице тогда, когда 2α=п/2, α=п/4. Таким образом, дальность полета максимальна в том случае, если тело бросить под углом 45°.

Это творческое задание для мастер-класса по информатике для школьников при ДВФУ.
Цель задания - выяснить, как изменится траектория тела, если учитывать сопротивление воздуха. Также необходимо ответить на вопрос, будет ли дальность полёта по-прежнему достигать максимального значения при угле бросания в 45°, если учитывать сопротивление воздуха.

В разделе "Аналитическое исследование" изложена теория. Этот раздел можно пропустить, но он должен быть, в основном, понятным для вас, потому что бо льшую часть из этого вы проходили в школе.
В разделе "Численное исследование" содержится описание алгоритма, который необходимо реализовать на компьютере. Алгоритм простой и краткий, поэтому все должны справиться.

Аналитическое исследование

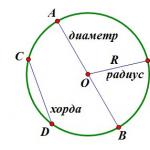
Введём прямоугольную систему координат так, как показано на рисунке. В начальный момент времени тело массой m находится в начале координат. Вектор ускорения свободного падения направлен вертикально вниз и имеет координаты (0, -g ).
- вектор начальной скорости. Разложим этот вектор по базису: . Здесь , где - модуль вектора скорости, - угол бросания.

Запишем второй закон Ньютона: .
Ускорение в каждый момент времени есть (мгновенная) скорость изменения скорости, то есть производная от скорости по времени: .

Следовательно, 2-й закон Ньютона можно переписать в следующем виде:
, где - это равнодействующая всех сил, действующая на тело.
Так как на тело действуют сила тяжести и сила сопротивления воздуха, то
.

Мы будем рассматривать три случая:
1) Сила сопротивления воздуха равна 0: .
2) Сила сопротивления воздуха противоположно направлена с вектором скорости, и её величина пропорциональна скорости: .
3) Сила сопротивления воздуха противоположно направлена с вектором скорости, и её величина пропорциональна квадрату скорости: .

Вначале рассмотрим 1-й случай.
В этом случае , или .


Из следует, что (равноускоренное движение).
Так как (r - радиус-вектор), то .
Отсюда .
Эта формула есть не что иное, как знакомая вам формула закона движения тела при равноускоренном движении.
Так как , то .
Учитывая, что и , получаем из последнего векторного равенства скалярные равенства:

Проанализируем полученные формулы.
Найдём время полёта тела. Приравняв y к нулю, получим

Дальность полёта равна значению координаты x в момент времени t 0:

Из этой формулы следует, что максимальная дальность полёта достигается при .
Теперь найдём уравнение трактории тела . Для этого выразим t через x

И подставим полученное выражение для t в равенство для y .

Полученная функция y (x ) -- квадратичная функция, её графиком является парабола, ветви которой направлены вниз.
Про движение тела, брошенного под углом к горизонту (без учёта сопротивления воздуха), рассказывается в этом видеоролике.

Теперь рассмотрим второй случай: .

Второй закон приобретает вид ,
отсюда .
Запишем это равенство в скалярном виде:

Мы получили два линейных дифференциальных уравнения .
Первое уравнение имеет решение

В чём можно убедиться, подставив данную функцию в уравнение для v x и в начальное условие .
Здесь e = 2,718281828459... -- число Эйлера .
Второе уравнение имеет решение

Так как , , то при наличии сопротивления воздуха движение тела стремится к равномерному, в отличие от случая 1, когда скорость неограниченно увеличивается.
В следующем видеоролике говорится, что парашютист сначала движется ускоренно, а потом начинает двигаться равномерно (даже до раскрытия парашюта).

Найдём выражения для x и y .
Так как x (0) = 0, y (0) = 0, то

Нам осталось рассмотреть случай 3, когда .
Второй закон Ньютона имеет вид
, или .
В скалярном виде это уравнение имеет вид:

Это система нелинейных дифференциальных уравнений . Данную систему не удаётся решить в явном виде, поэтому необходимо применять численное моделирование.

Численное исследование

В предыдущем разделе мы увидели, что в первых двух случаях закон движения тела можно получить в явном виде. Однако в третьем случае необходимо решать задачу численно. При помощи численных методов мы получим лишь приближённое решение, но нас вполне устроит и небольшая точность. (Число π или квадратный корень из 2, кстати, нельзя записать абсолютно точно, поэтому при расчётах берут какое-то конечное число цифр, и этого вполне хватает.)

Будем рассматривать второй случай, когда сила сопротивления воздуха определяется формулой. Отметим, что при k = 0 получаем первый случай.

Скорость тела подчиняется следующим уравнениям:

В левых частях этих уравнений записаны компоненты ускорения .
Напомним, что ускорение есть (мгновенная) скорость изменения скорости, то есть производная от скорости по времени.
В правых частях уравнений записаны компоненты скорости. Таким образом, данные уравнения показывают, как скорость изменения скорости связана со скоростью.

Попробуем найти решения этих уравнений при помощи численных методов. Для этого введём на временной оси сетку : выберем число и будем рассматривать моменты времени вида : .

Наша задача -- приближённо вычислить значения в узлах сетки.

Заменим в уравнениях ускорение (мгновенную скорость изменения скорости) на среднюю скорость изменения скорости, рассматривая движение тела на промежутке времени :

Теперь подставим полученные аппроксимации в наши уравнения.

Полученные формулы позволяют нам вычислить значения функций в следующем узле сетки, если известны значения этих функций в предыдущем узле сетки.

При помощи описанного метода мы можем получить таблицу приближённых значений компонент скорости.

Как найти закон движения тела, т.е. таблицу приближённых значений координат x (t ), y (t )? Аналогично!
Имеем

Значение vx[j] равняется значению функции , для других массивов аналогично.
Теперь остаётся написать цикл, внутри которого мы будем вычислять vx через уже вычисленное значение vx[j], и с остальными массивами то же самое. Цикл будет по j от 1 до N .
Не забудьте инициализировать начальные значения vx, vy, x, y по формулам , x 0 = 0, y 0 = 0.

В Паскале и Си для вычисления синуса и косинуса имеются функции sin(x) , cos(x) . Обратите внимание, что эти функции принимают аргумент в радианах.

Вам необходимо построить график движения тела при k = 0 и k > 0 и сравнить полученные графики. Графики можно построить в Excel.
Отметим, что расчётные формулы настолько просты, что для вычислений можно использовать один только Excel и даже не использовать язык программирования.
Однако в дальнейшем вам нужно будет решить задачу в CATS, в которой нужно вычислить время и дальность полёта тела, где без языка программирования не обойтись.

Обратите внимание, что вы можете протестировать вашу программу и проверить ваши графики, сравнив результаты вычислений при k = 0 с точными формулами, приведёнными в разделе "Аналитическое исследование".

Поэкспериментируйте со своей программой. Убедитесь в том, что при отсутствии сопротивления воздуха (k = 0) максимальная дальность полёта при фиксированной начальной скорости достигается при угле в 45°.
А с учётом сопротивления воздуха? При каком угле достигается максимальная дальность полёта?

На рисунке представлены траектории тела при v 0 = 10 м/с, α = 45°, g = 9,8 м/с 2 , m = 1 кг, k = 0 и 1, полученные при помощи численного моделирования при Δt = 0,01.

Вы можете ознакомиться с замечательной работой 10-классников из г. Троицка, представленной на конференции "Старт в науку" в 2011 г. Работа посвящена моделированию движения теннисного шарика, брошенного под углом к горизонту (с учетом сопротивления воздуха). Применяется как численное моделирование, так и натурный эксперимент.

Таким образом, данное творческое задание позволяет познакомиться с методами математического и численного моделирования, которые активно используются на практике, но мало изучаются в школе. К примеру, данные методы использовались при реализации атомного и космического проектов в СССР в середине XX века.

Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила -- сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения; проекции ускорения на координатные оси ах = 0, ау = - g.

Рисунок 1. Кинематические характеристики тела, брошенного под углом к горизонту

Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1).

Проекции скорости тела, следовательно, изменяются со временем следующим образом:

где $v_0$ - начальная скорость, ${\mathbf \alpha }$ - угол бросания.

При нашем выборе начала координат начальные координаты (рис. 1) $x_0=y_0=0$. Тогда получим:

(1)

Проанализируем формулы (1). Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета:

Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т.е. это значение также имеет физический смысл.

Дальность полета получим из первой формулы (1). Дальность полета - это значение координаты х в конце полета, т.е. в момент времени, равный $t_0$. Подставляя значение (2) в первую формулу (1), получаем:

Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.

Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем

Из уравнений (1) можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения (1) выразить время:

и подставить его во второе уравнение. Тогда получим:

Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания $\alpha $ и его функции -- здесь просто константы, т.е. постоянные числа.

Тело брошено со скоростью v0 под углом ${\mathbf \alpha }$ к горизонту. Время полета $t = 2 с$. На какую высоту Hmax поднимется тело?

$$t_В = 2 с$$ $$H_max - ?$$

Закон движения тела имеет вид:

$$\left\{ \begin{array}{c} x=v_{0x}t \\ y=v_{0y}t-\frac{gt^2}{2} \end{array} \right.$$

Вектор начальной скорости образует с осью ОХ угол ${\mathbf \alpha }$. Следовательно,

\ \ \

С вершины горы бросают под углом = 30${}^\circ$ к горизонту камень с начальной скоростью $v_0 = 6 м/с$. Угол наклонной плоскости = 30${}^\circ$. На каком расстоянии от точки бросания упадет камень?

$$ \alpha =30{}^\circ$$ $$v_0=6\ м/с$$ $$S - ?$$

Поместим начало координат в точку бросания, ОХ -- вдоль наклонной плоскости вниз, OY -- перпендикулярно наклонной плоскости вверх. Кинематические характеристики движения:

Закон движения:

$$\left\{ \begin{array}{c} x=v_0t{cos 2\alpha +g\frac{t^2}{2}{sin \alpha \ }\ } \\ y=v_0t{sin 2\alpha \ }-\frac{gt^2}{2}{cos \alpha \ } \end{array} \right.$$ \

Подставив полученное значение $t_В$, найдём $S$: